pacman::p_load(sf, tmap, tidyverse)Hands-on Exercise 7c: Analytical Mapping
1 Overview
In this in-class exercise, we will gain hands-on experience on using appropriate R methods to plot analytical maps.
2 Getting Started
2.1 Loading Packages
In this exercise, we will be using the following packages:
| Package | Description |
|---|---|
| tmap | For choropleth mapping. |
| tidyverse | readr: For importing delimited text file. tidyr: For tidying data. dplyr: For data wrangling. |
| sf | For handling geospatial data. |
| knitr | For html tables |
2.2 Importing Data
For the purpose of this hands-on exercise, a prepared data set called NGA_wp.rds will be used. The data set is a polygon feature data.frame providing information on water point of Nigeria at the LGA level.
NGA_wp <- read_rds("data/rds/NGA_wp.rds")| Function | Package | Description | Output |
|---|---|---|---|
read_rds() |
readr | Import NGA_wp.rds into R | R object |
2.3 Checking the Data
list(head(NGA_wp, 5))[[1]]
Simple feature collection with 5 features and 8 fields
Geometry type: MULTIPOLYGON
Dimension: XY
Bounding box: xmin: 481088 ymin: 98142.39 xmax: 1248985 ymax: 1079710
Projected CRS: Minna / Nigeria Mid Belt
ADM2_EN ADM2_PCODE ADM1_EN ADM1_PCODE
1 Aba North NG001001 Abia NG001
2 Aba South NG001002 Abia NG001
3 Abadam NG008001 Borno NG008
4 Abaji NG015001 Federal Capital Territory NG015
5 Abak NG003001 Akwa Ibom NG003
geometry total_wp wp_functional wp_nonfunctional
1 MULTIPOLYGON (((548795.5 11... 17 7 9
2 MULTIPOLYGON (((547286.1 11... 71 29 35
3 MULTIPOLYGON (((1248985 104... 0 0 0
4 MULTIPOLYGON (((510864.9 57... 57 23 34
5 MULTIPOLYGON (((594269 1209... 48 23 25
wp_unknown
1 1
2 7
3 0
4 0
5 03 Choropleth Mapping to visualise distribution of non-functional water points
tmap_mode("plot")
p1 <- tm_shape(NGA_wp)+
tm_fill("total_wp",
n= 10,
style = "equal",
palette = "Purples") +
tm_borders(lwd = 0.1,
alpha = 0.5) +
tm_layout(main.title = "Distribution of total water point by LGAs",
main.title.size = 1,
main.title.position = "center",
legend.position = c("right", "bottom"),
legend.height = .45,
legend.width = .2,
frame = FALSE,
bg.color = "#f5f5f5")
p2 <- tm_shape(NGA_wp)+
tm_fill("wp_functional",
n=10,
style="equal",
palette ="Blues") +
tm_borders(lwd = 0.1,
alpha = 0.5) +
tm_layout(main.title = "Distribution of functional water point by LGAs",
main.title.size = 1,
main.title.position = "center",
legend.position = c("right", "bottom"),
legend.height = .4,
legend.width = .2,
frame = FALSE,
bg.color = "#f5f5f5")
tmap_arrange(p1, p2, nrow =1, ncol =2)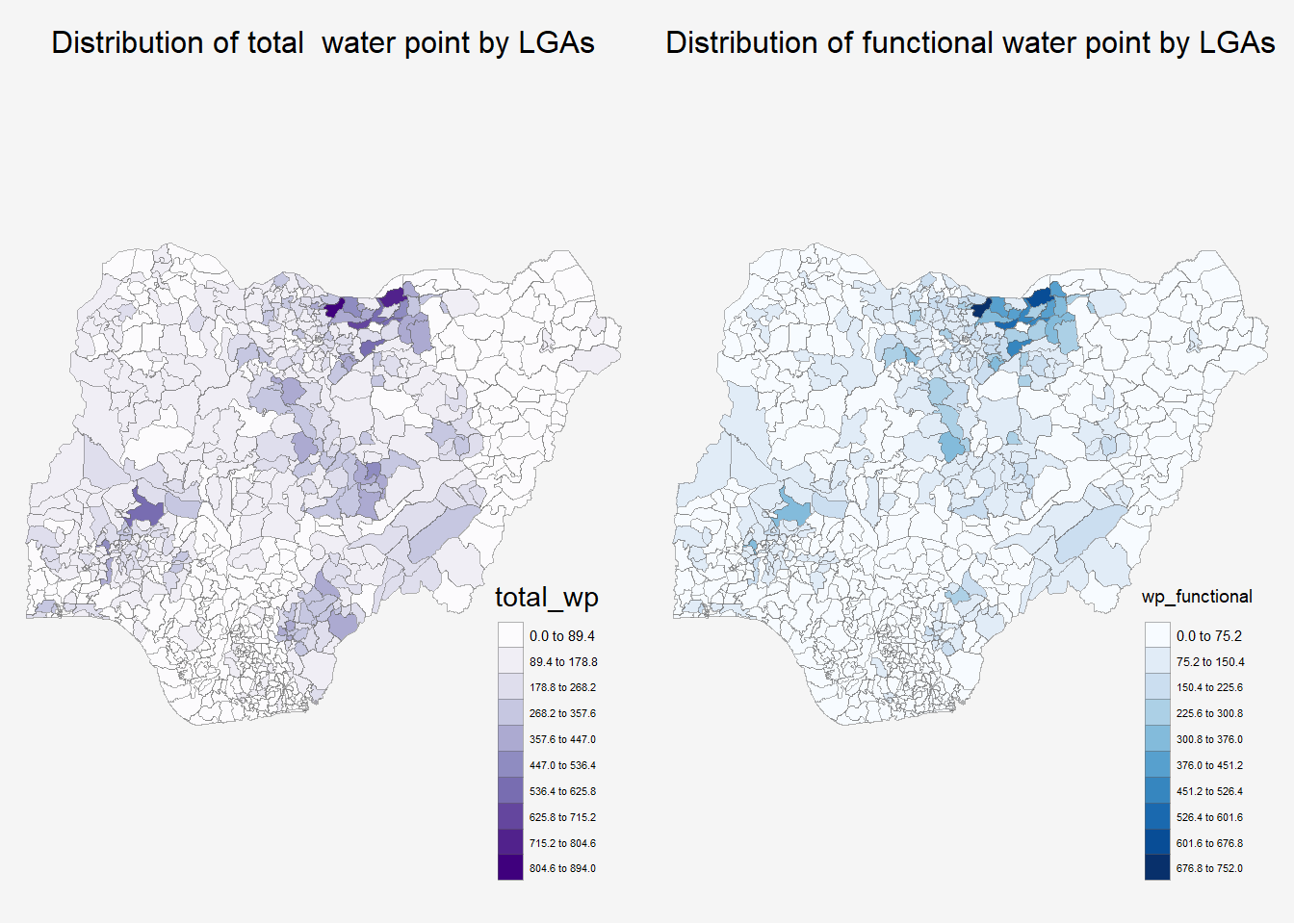
4 Choropleth Maps for Rates
In much of our readings we have now seen the importance to map rates rather than counts of things, and that is for the simple reason that water points are not equally distributed in space. That means that if we do not account for how many water points are somewhere, we end up mapping total water point size rather than our topic of interest.
4.1 Deriving Proportion of Functional Water Points and Non-Functional Water Points
We will tabulate the proportion of functional water points and the proportion of non-functional water points in each LGA. In the following code chunk, mutate() from dplyr package is used to derive two fields, namely pct_functional and pct_nonfunctional.
NGA_wp2 <- NGA_wp %>%
mutate(pct_functional = wp_functional/total_wp) %>%
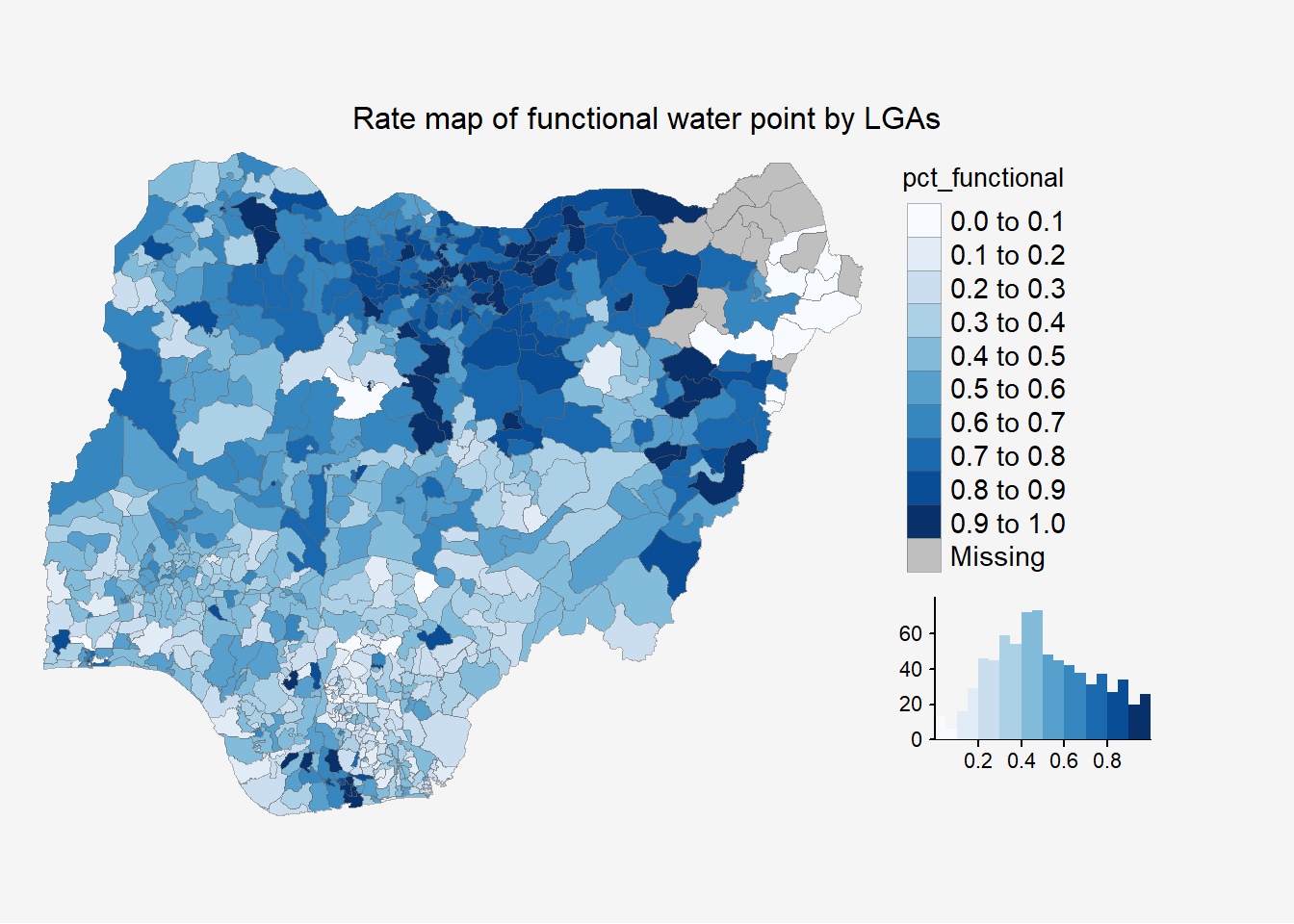
mutate(pct_nonfunctional = wp_nonfunctional/total_wp)4.2 Plotting map of rate
tm_shape(NGA_wp2) +
tm_fill("pct_functional",
n = 10,
style = "equal",
palette = "Blues",
legend.hist = TRUE) +
tm_borders(lwd = 0.1,
alpha = .5) +
tm_layout(main.title = "Rate map of functional water point by LGAs",
main.title.size = 1,
main.title.position = "center",
legend.outside = TRUE,
frame = FALSE,
bg.color = "#f5f5f5",
legend.text.size = 1,
legend.hist.width = 0.7
)
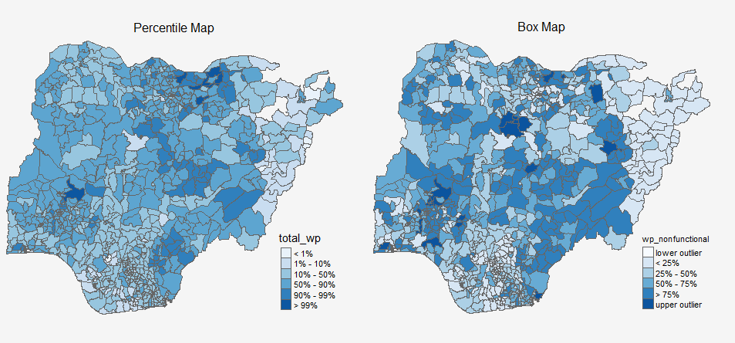
8 Extreme Value Maps
Extreme value maps are variations of common choropleth maps where the classification is designed to highlight extreme values at the lower and upper end of the scale, with the goal of identifying outliers. These maps were developed in the spirit of spatializing EDA, i.e., adding spatial features to commonly used approaches in non-spatial EDA (Anselin 1994).
8.1 Percentile Map
The percentile map is a special type of quantile map with six specific categories: 0-1%, 1-10%, 10-50%, 50-90%, 90-99%, and 99-100%. The corresponding breakpoints can be derived by means of the base R quantile command, passing an explicit vector of cumulative probabilities as c(0, .01, .1, .5, .9, .99, 1). Note that the begin and endpoint need to be included.
8.1.1 Data Preparation
Step 1: Exclude records with NA
NGA_wp3 <- NGA_wp2 %>%
drop_na()Step 2: Creating customised classification and extracting values
percent <- c(0,.01,.1,.5,.9,.99,1)
var <- NGA_wp3["pct_functional"] %>%
st_set_geometry(NULL) #<< Drops geometry field
quantile(var[,1], percent) 0% 1% 10% 50% 90% 99% 100%
0.0000000 0.0000000 0.2169811 0.4791667 0.8611111 1.0000000 1.0000000 8.1.2 Creating the get.var function
get.var <- function(vname,df) {
v <- df[vname] %>%
st_set_geometry(NULL)
v <- unname(v[,1])
return(v)
}Firstly, we will write an R function as shown below to extract a variable (i.e. wp_nonfunctional) as a vector out of an sf data.frame.
- arguments:
- vname: variable name (as character, in quotes)
- df: name of sf data frame
- returns:
- v: vector with values (without a column name)
8.1.3 A percentile mapping function
Next, we will write a percentile mapping function by using the code chunk below.
percentmap <- function(vnam, df, legtitle=NA, mtitle="Percentile Map"){
percent <- c(0,.01,.1,.5,.9,.99,1)
var <- get.var(vnam, df)
bperc <- quantile(var, percent)
tm_shape(df) +
tm_polygons() +
tm_shape(df) +
tm_fill(vnam,
title=legtitle,
breaks=bperc,
palette="Blues",
labels=c("< 1%", "1% - 10%", "10% - 50%", "50% - 90%", "90% - 99%", "> 99%")) +
tm_borders() +
tm_layout(main.title = mtitle,
title.position = c("right","bottom"),
main.title.size = 1,
main.title.position = "center",
frame = FALSE,
bg.color = "#f5f5f5",)
}8.1.4 The End Product
percentmap("total_wp", NGA_wp3)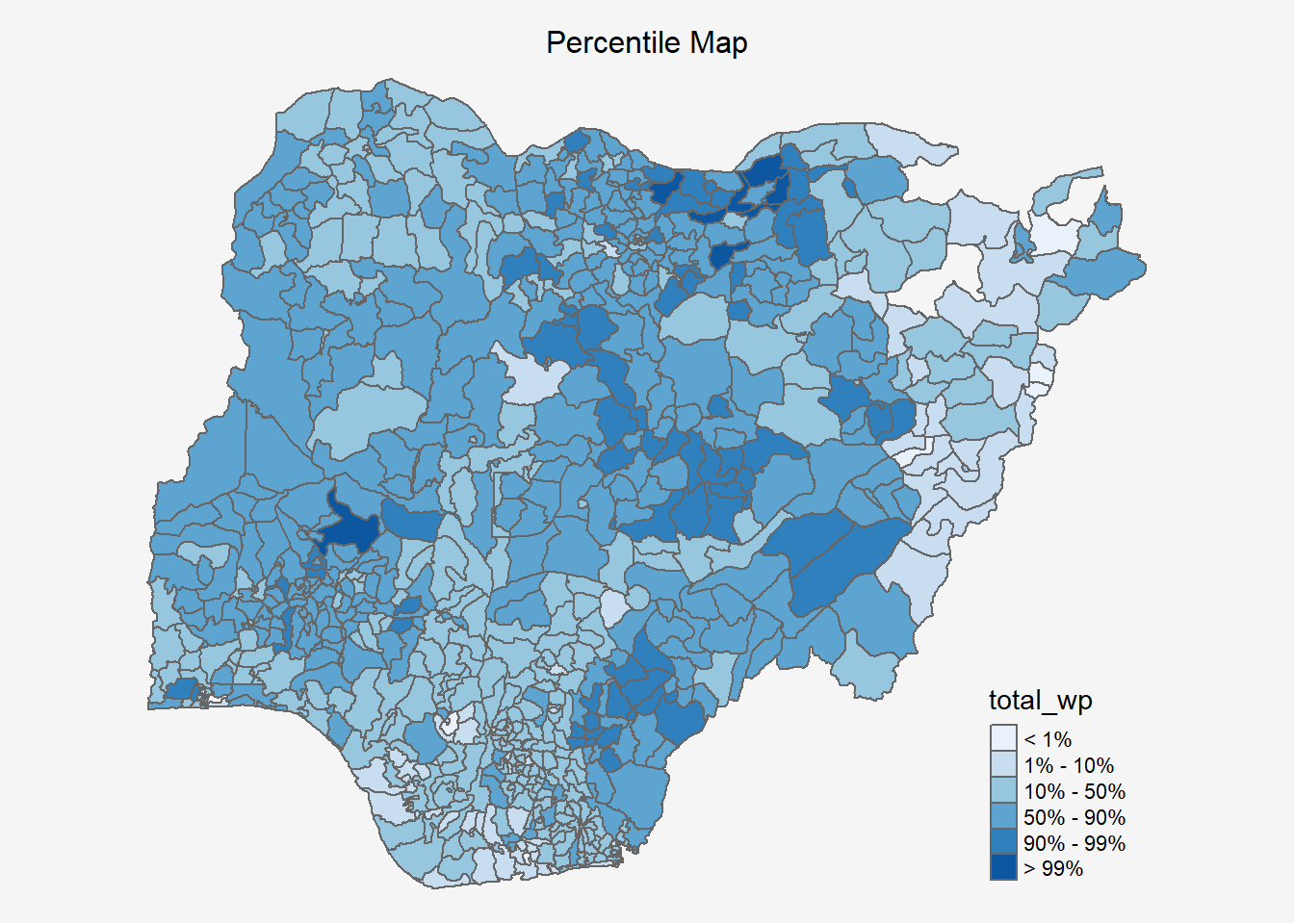
8.1.5 Comparison of maps with and without dropping NAs
tmap_arrange(percentmap("total_wp", NGA_wp3),
percentmap("total_wp", NGA_wp2),
nrow =1,
ncol =2)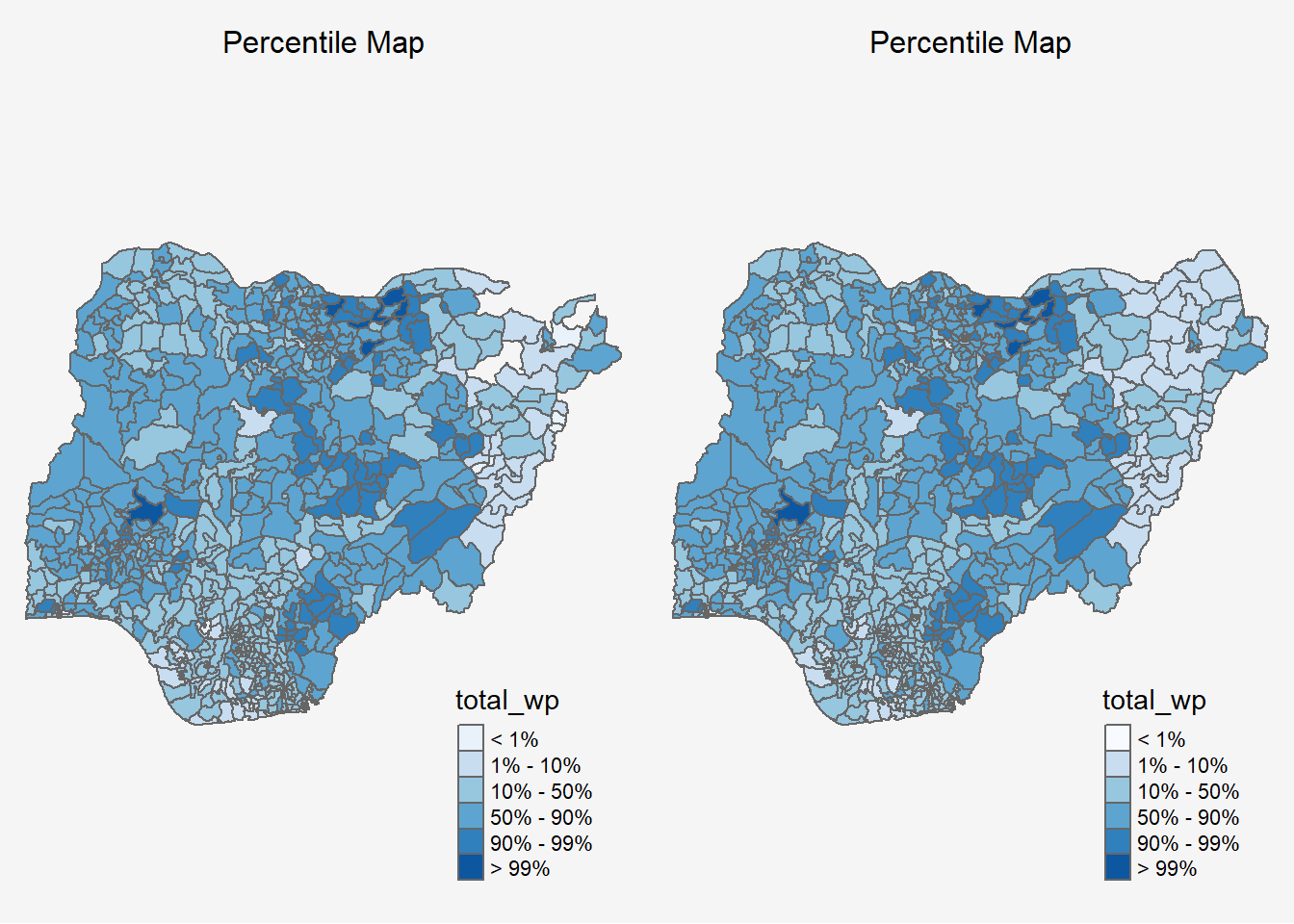
8.2 Box Map
In essence, a box map is an augmented quartile map, with an additional lower and upper category. When there are lower outliers, then the starting point for the breaks is the minimum value, and the second break is the lower fence. In contrast, when there are no lower outliers, then the starting point for the breaks will be the lower fence, and the second break is the minimum value (there will be no observations that fall in the interval between the lower fence and the minimum value).
Displaying summary statistics on a choropleth map by using the basic principles of boxplot.
To create a box map, a custom breaks specification will be used. However, there is a complication. The break points for the box map vary depending on whether lower or upper outliers are present.
8.2.1 Creating the boxbreaks function
The code chunk below is an R function that creating break points for a box map.
- arguments:
- v: vector with observations
- mult: multiplier for IQR (default 1.5)
- returns:
- bb: vector with 7 break points compute quartile and fences
boxbreaks <- function(v,mult=1.5) {
qv <- unname(quantile(v))
iqr <- qv[4] - qv[2]
upfence <- qv[4] + mult * iqr #<< Q3 + 1.5*IQR = Left end of whister
lofence <- qv[2] - mult * iqr #<< Q1 - 1.5*IQR = Right end of the whisker
# initialize break points vector
bb <- vector(mode="numeric",length=7)
# logic for lower and upper fences
if (lofence < qv[1]) { # no lower outliers
bb[1] <- lofence
bb[2] <- floor(qv[1])
} else {
bb[2] <- lofence
bb[1] <- qv[1]
}
if (upfence > qv[5]) { # no upper outliers
bb[7] <- upfence
bb[6] <- ceiling(qv[5])
} else {
bb[6] <- upfence
bb[7] <- qv[5]
}
bb[3:5] <- qv[2:4]
return(bb)
}8.2.2 Creating the get.var function
get.var <- function(vname,df) {
v <- df[vname] %>% st_set_geometry(NULL)
v <- unname(v[,1])
return(v)
}var <- get.var("wp_nonfunctional", NGA_wp3)
boxbreaks(var)[1] -56.5 0.0 14.0 34.0 61.0 131.5 278.08.2.3 The boxmap function
boxmap <- function(vnam, df,
legtitle=NA,
mtitle="Box Map",
mult=1.5){
var <- get.var(vnam,df)
bb <- boxbreaks(var)
tm_shape(df) +
tm_polygons() +
tm_shape(df) +
tm_fill(vnam,title=legtitle,
breaks=bb,
palette="Blues",
labels = c("lower outlier",
"< 25%",
"25% - 50%",
"50% - 75%",
"> 75%",
"upper outlier")) +
tm_borders() +
tm_layout(main.title = mtitle,
title.position = c("left","top"),
main.title.size = 1,
main.title.position = "center",
frame = FALSE,
bg.color = "#f5f5f5",
legend.title.size = 0.8)
}8.2.4 The End Product
tmap_mode("plot")
boxmap("wp_nonfunctional", NGA_wp3)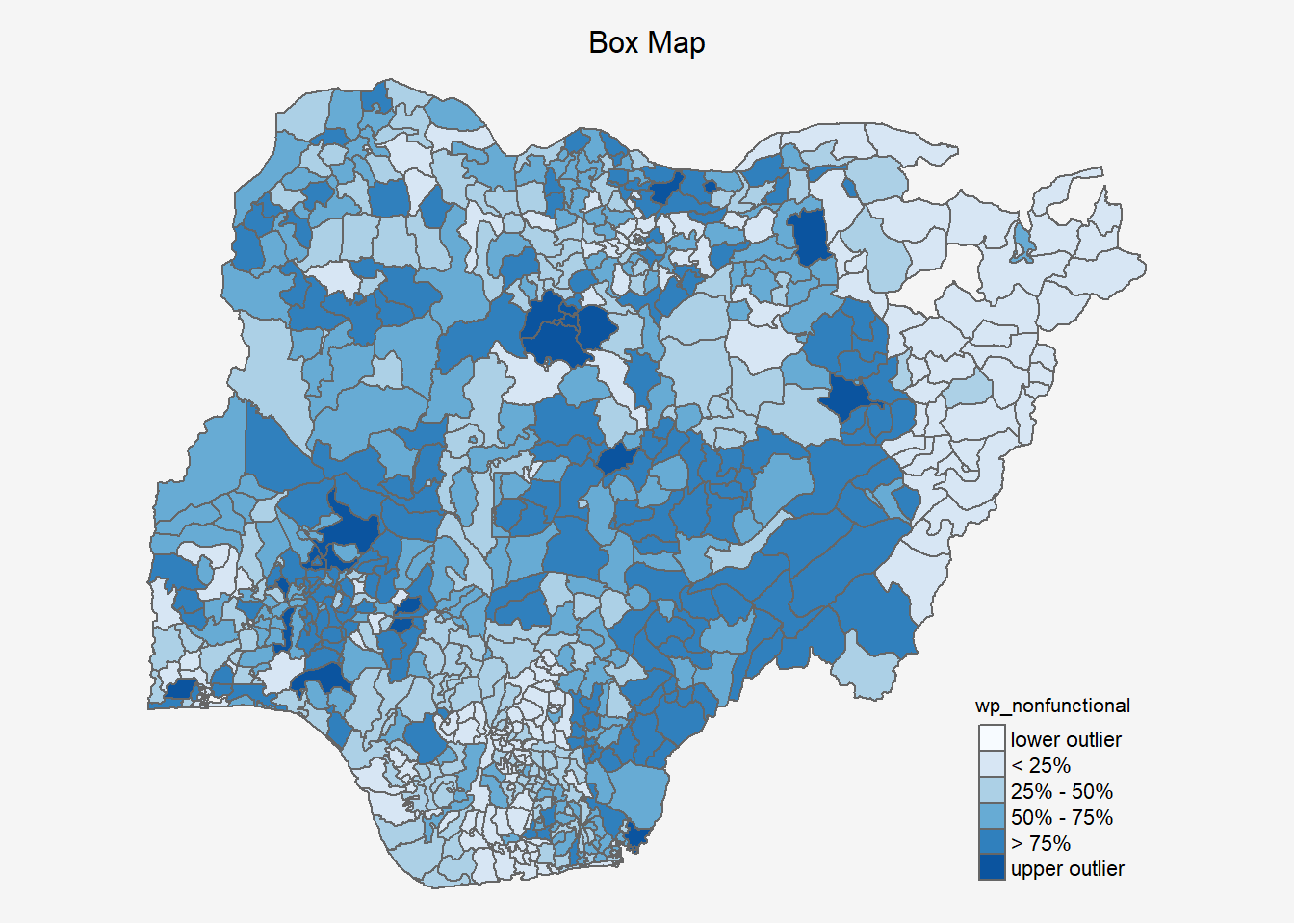
7 Reference
- Kam, T.S. (2023). Analytical Mapping.